Flip-flops
Table of contents
- Flip-flops
- Introduction
- Differences between latches and flip-flops
- Sub-modules
- Introduction
- State table
- Characteristic table
- Introduction
- State table
- Introduction
- State table
- Characteristic table
- Introduction
- State table
- Characteristic table
- Introduction
- Master-slave JK flip-flop constructed by using NAND gates
- State table
- Characteristic table
- Excitation table
- Characteristic equation
- Flip-flops interaction
Flip-flops
Introduction
You covered about latches in the previous modules. Those are the basic building blocks of flip-flops. You can implement flip-flops in two methods.
In first method, cascade two latches in such a way that the first latch is enabled for every positive clock pulse and second latch is enabled for every negative clock pulse. So that the combination of these two latches become a flip-flop.
In second module, you can directly implement the flip-flop, which is edge sensitive. In this module, let us discuss the following flip-flops using second method.
Differences between latches and flip-flops
| Latches | Flip-flops |
|---|---|
| Level triggered | Edge triggered |
| Asynchronous device | Synchronous device |
| Doesn’t contain clock signal | Contains a clock signal |
| It will change its state as long as it is enabled | It will change its state only during a given clock cycle |
| Consumes less power | Consumes more power |
| Faster | Slower |
| Examples: D-Latch, T-Latch | Examples: D-Flip flop, T-Flop flop |
Sub-modules
Now let us implement various flip-flops by providing the cross coupling between NOR gates. You can also implement these flip-flops by using NAND gates, as well.
SR flip-flop
Introduction
SR flip-flop operates with only positive clock transitions or negative clock transitions. Whereas, SR latch operates with enable signal. The circuit diagram of SR flip-flop is shown in the following figure.
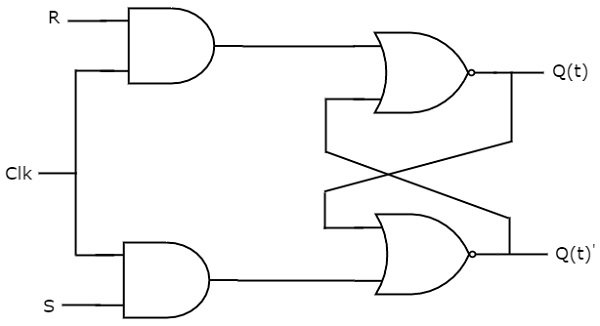
his circuit has two inputs S & R and two outputs Q(t) & Q(t)’. The operation of SR flipflop is similar to SR Latch. But, this flip-flop affects the outputs only when positive transition of the clock signal is applied instead of active enable.
State table
| S | R | Q(t+1) |
|---|---|---|
| 0 | 0 | Q(t) |
| 0 | 1 | 0 |
| 1 | 0 | 1 |
| 1 | 1 | - |
Here, Q(t) & Q(t + 1) are present state & next state respectively. So, SR flip-flop can be used for one of these three functions such as Hold, Reset & Set based on the input conditions, when positive transition of clock signal is applied.
Characteristic table
Therefore, SR Latch performs three types of functions such as Hold, Set & Reset based on the input conditions.
| S | R | Q(t) | Q(t+1) |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | x |
| 1 | 1 | 1 | x |
By using three variable K-Map, you can get the simplified expression for next state, Q(t + 1). The three variable K-Map for next state, Q(t + 1) is shown in the following figure.
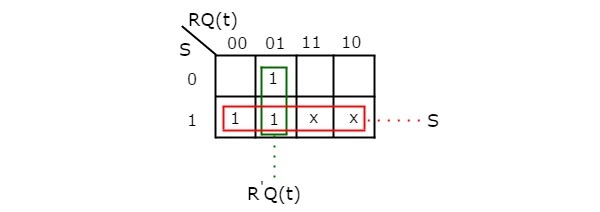
The maximum possible groupings of adjacent ones are already shown in the figure. Therefore, the simplified expression for next state Q(t + 1) is
Q(t + 1) = S + R'.Q(t)
D flip-flop
Introduction
D flip-flop operates with only positive clock transitions or negative clock transitions. Whereas, D latch operates with enable signal. That means, the output of D flip-flop is insensitive to the changes in the input, D except for active transition of the clock signal. The circuit diagram of D flip-flop is shown in the following figure.
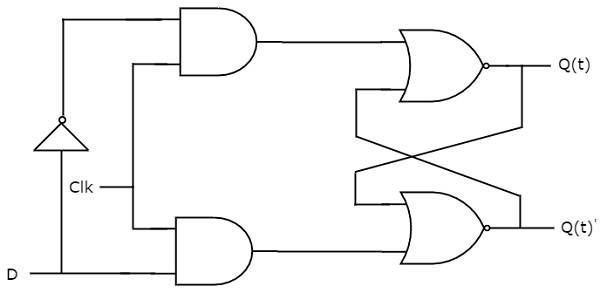
This circuit has single input D and two outputs Q(t) & Q(t)’. The operation of D flip-flop is similar to D Latch. But, this flip-flop affects the outputs only when positive transition of the clock signal is applied instead of active enable.
State table
| D | Q(t+1) |
|---|---|
| 0 | 0 |
| 1 | 1 |
Therefore, D flip-flop always Hold the information, which is available on data input, D of earlier positive transition of clock signal. From the above state table, the next state equation can be directly written as
Q(t + 1) = D
Next state of D flip-flop is always equal to data input, D for every positive transition of the clock signal. Hence, D flip-flops can be used in registers, shift registers and some of the counters.
JK flip-flop
Introduction
JK flip-flop is the modified version of SR flip-flop. It operates with only positive clock transitions or negative clock transitions. The circuit diagram of JK flip-flop is shown in the following figure.
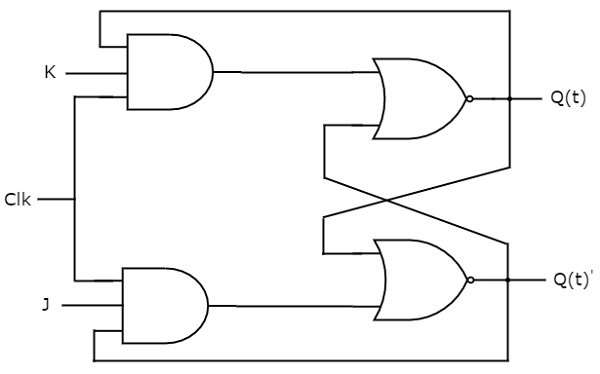
This circuit has two inputs J & K and two outputs Q(t) & Q(t)’. The operation of JK flip-flop is similar to SR flip-flop. Here, the inputs of SR flip-flop are considered as S = J Q(t)’ and R = KQ(t) in order to utilize the modified SR flip-flop for 4 combinations of inputs.
State table
| J | K | Q(t+1) |
|---|---|---|
| 0 | 0 | Q(t) |
| 0 | 1 | 0 |
| 1 | 0 | 1 |
| 1 | 1 | Q(t)’ |
Here, Q(t) & Q(t + 1) are present state & next state respectively. So, JK flip-flop can be used for one of these four functions such as Hold, Reset, Set & Complement of present state based on the input conditions, when positive transition of clock signal is applied.
Characteristic table
| J | K | Q(t) | Q(t+1) |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 0 |
By using three variable K-Map, you can get the simplified expression for next state, Q(t + 1). The three variable K-Map for next state, Q(t + 1) is shown in the following figure.
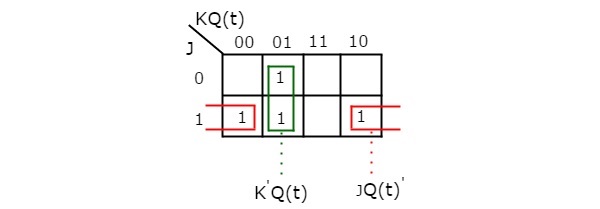
The maximum possible groupings of adjacent ones are already shown in the figure. Therefore, the simplified expression for next state Q(t+1) is
Q(t + 1) = J.Q(t)' + K'.Q(t)
T flip-flop
Introduction
T flip-flop is the simplified version of JK flip-flop. It is obtained by connecting the same input ‘T’ to both inputs of JK flip-flop. It operates with only positive clock transitions or negative clock transitions. The circuit diagram of T flip-flop is shown in the following figure.
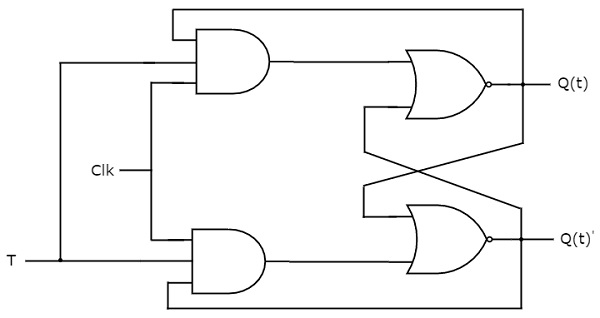
This circuit has single input T and two outputs Q(t) & Q(t)’. The operation of T flip-flop is same as that of JK flip-flop. Here, the inputs of JK flip-flop are considered as J = T and K = T in order to utilize the modified JK flip-flop for 2 combinations of inputs. So, the other two combinations of J & K are eliminated, for which those two values are complement to each other in T flip-flop.
State table
| D | Q(t+1) |
|---|---|
| 0 | Q(t) |
| 1 | Q(t)’ |
Here, Q(t) & Q(t + 1) are present state & next state respectively. So, T flip-flop can be used for one of these two functions such as Hold, & Complement of present state based on the input conditions, when positive transition of clock signal is applied.
Characteristic table
| T | Q(t) | Q(t + 1) |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
From the above characteristic table, the next state equation can be directly written as:
Q(t + 1) = T'.Q(t) + T.Q(t)'
=> Q(t + 1) = T ⊕ Q(t)
The output of T flip-flop always toggles for every positive transition of the clock signal, when input T remains at logic High (1). Hence, T flip-flop can be used in counters.
Master-slave JK flip-Flop
Introduction
Master-slave JK flip-flop is designed to eliminate the race around condition in JK flip-flop and it is constructed by using two JK flip-flops as shown in the circuit diagram below.
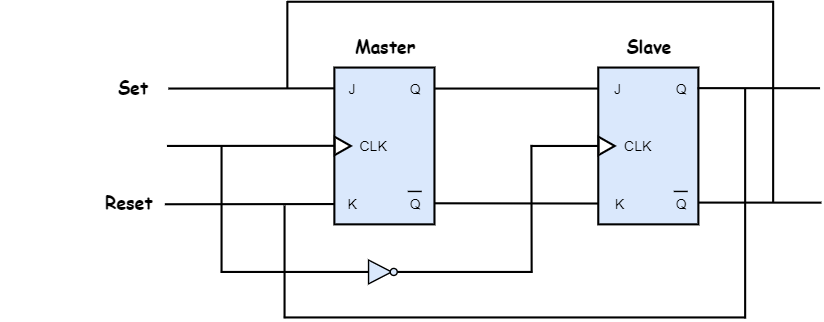
The first flip-flop is called the master, and it is driven by the positive clock cycle. The second flip-flop is called the slave, and it is driven by the negative clock cycle. During the positive clock cycle, master flip-flop gives the intermediate output but slave flip-flop will not give the final output. During the negative clock cycle, slave flip-flop gets activated and copies the previous output of the master flip-flop and produces the final output.
Master-slave JK flip-flop constructed by using NAND gates
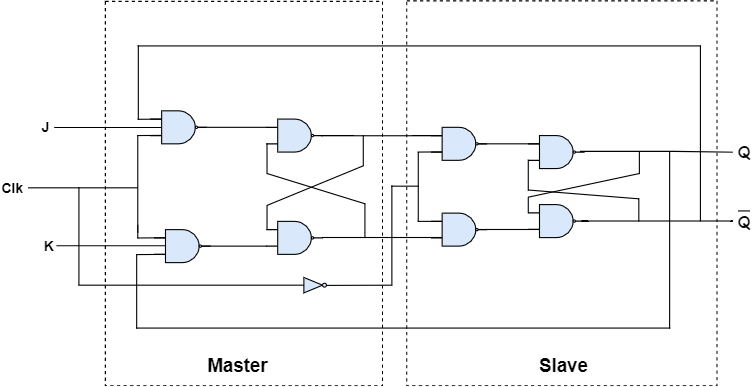
State table
| Clock | J | K | Q(n+1) | Comments |
|---|---|---|---|---|
| 0 | X | X | Q(n) | No change |
| 1 | 0 | 0 | Q(n) | No change |
| 1 | 0 | 1 | 0 | Reset |
| 1 | 1 | 0 | 1 | Set |
| 1 | 1 | 1 | Q(n)’ | Toggle |
Here, Q(n) is the present state and Q(n+1) is the next state.
Characteristic table
| Q(n) | J | K | Q(n+1) |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 0 |
Excitation table
| Q(n) | Q(n+1) | J | K |
|---|---|---|---|
| 0 | 0 | 0 | X |
| 0 | 1 | 1 | X |
| 1 | 0 | X | 1 |
| 1 | 1 | X | 0 |
Characteristic equation
Q(n+1) = Q(n)'J + Q(n)K'
Flip-flops interaction
"A State Table is a tabular representation of the time sequence of inputs, outputs, and flip-flop states. The table consists of four sections marked as present table, next state, and the output. The present-state section shows the states of flip-flops at any given time t. The input section gives a value for each possible present state. The next-state section lists the state of flip-flops one clock period later at time t + 1. Lastly, the output section gives the value for each present state."
Feel free to review your input before generating your state table.